Ciąg Fibonacciego

Ciąg Fibonacciego jest ciągiem rekurencyjnym. Każdy wyraz, oprócz dwóch pierwszych jest sumą dwóch poprzednich wyrazów. Pierwszy i drugi element ciągu jest równy 1, a każdy następny otrzymujemy dodając do siebie dwa poprzednie.

Matematycznie wygląda to następująco:

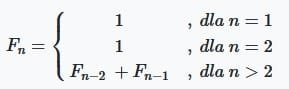
Zgodnie z matematyczną teorią F (n) = F (n-2) + F (n-1) dla dowolnego i > 0,

Kilka kolejnych wyrazów tego ciągu przedstawia się następująco:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …

Rozwiązanie Rekurencyjne:

private static int fib(int i)
{
   if (i <= 2)
   {                
      return 1;
   }                
   return fib(i - 2) + fib(i - 1);
}

• podstawowy przypadek funkcji rekurencyjnej dla 1 i 2 numery sekwencji Fibonacciego to 1, czyli zwracamy 1
• przypadek rekurencyjny, zwracamy sumę dwóch poprzednich liczb Fibonacciego
• to działa, ponieważ definicja sekwencji Fibonacciego określa, że suma dwóch sąsiednich elementów jest równa kolejnemu elementowi

Rozwiązanie to możemy skrócić do jednej linijki

 private static int fib(int n)
 {
    return (n <= 2) ? 1 : fib(n - 1) + fib(n - 2);
 }

Pod względem efektywności taki kod nie jest najlepszym rozwiązaniem, ponieważ zużywa bardzo dużo pamięci. Podczas każdego wywołania funkcji deklarowane są kolejne zmienne, które są zwalnianie dopiero jak funkcja zwróci wartość.

Dlatego w tym wypadku lepszym rozwiązaniem będzie rozwiązanie iteracyjne:

Rozwiązanie Iteracyjne:

private static int fib(int n)
{
   int a = 0, b = 1;

   for (int i = 0; i < n; i++)
   {
      b = a + b;        // można skrócić   b += a;         
      a = b - a;      
   }
   return a;
}

• pod zmienną b przypisujemy wyraz następny czyli a + b
• pod zmienną a przypisujemy wartość zmiennej b czyli b – a

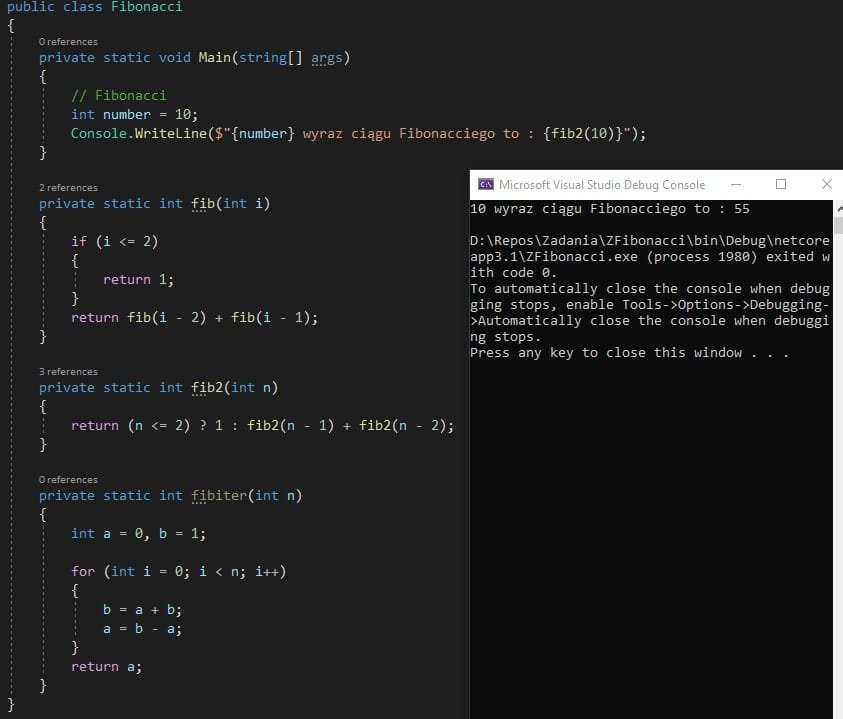
I teraz sprawdzamy nasze rozwiązania.

static void Main(string[] args)
{
   // Fibonacci
   int number = 10;
   Console.WriteLine($"{number} wyraz ciągu Fibonacciego to : {fib(10)}");
}